Josephood7

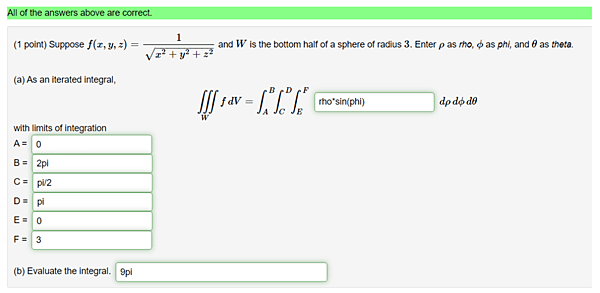
 Suppose [math] and [math] is the bottom half of a sphere of radius [math]. Enter [math] as rho, [math] as phi, and [math] as theta.

(a) As an iterated integral,

with limits of integration
A = 
B = 
C = 
D = 
E = 
F = 

(b) Evaluate the integral. 

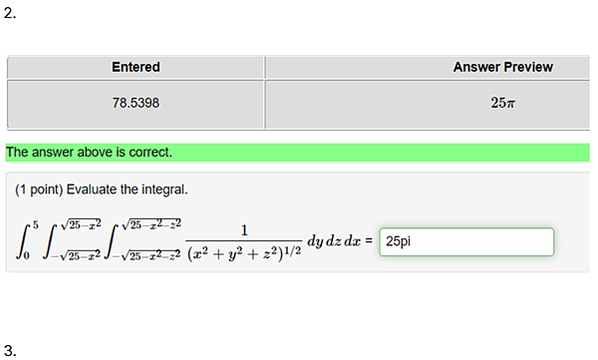
Evaluate the integral.

[math] = 

Note: You can earn partial credit on this problem.

Write a triple integral including limits of integration that gives the volume of the cap of the solid sphere [math] cut off by the plane [math] and restricted to the first octant. (In your integral, use theta, rho, and phi for [math], [math] and [math], as needed.)

What coordinates are you using? 
(Enter cartesian, cylindrical, or spherical.)

With [math] , [math] ,
[math] , [math] ,
[math] , and [math] ,
Volume = [math] [math] [math] [math]

Solution: