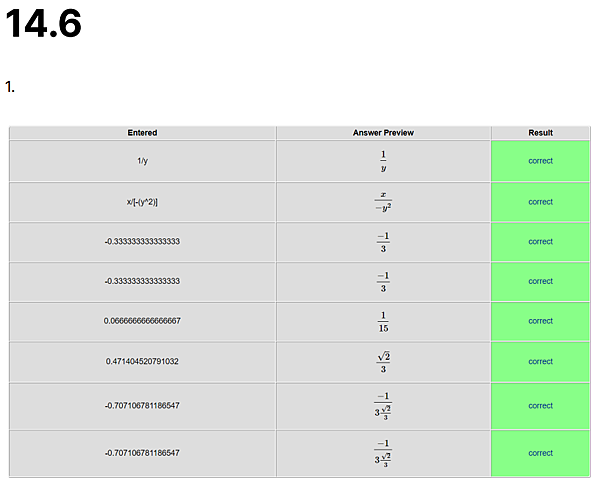
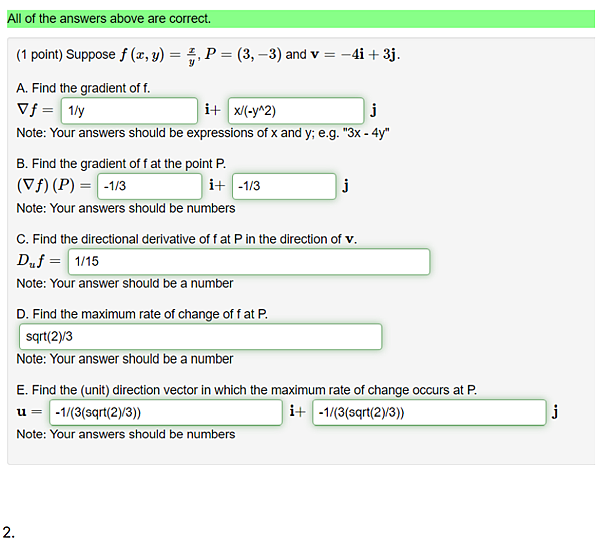
Suppose [math], [math] and [math].
A. Find the gradient of f.
[math] [math] [math]
Note: Your answers should be expressions of x and y; e.g. "3x - 4y"
B. Find the gradient of f at the point P.
[math] [math] [math]
Note: Your answers should be numbers
C. Find the directional derivative of f at P in the direction of [math].
[math]
Note: Your answer should be a number
D. Find the maximum rate of change of f at P.
Note: Your answer should be a number
E. Find the (unit) direction vector in which the maximum rate of change occurs at P.
[math] [math] [math]
Note: Your answers should be numbers
Note: You can earn partial credit on this problem.
For each of the following pairs of functions [math] and [math], determine if the level curves of the functions cross at right angles, and find their gradients at the indicated point.
(a) [math], [math].
Do the level curves of [math] and [math] cross at right angles?
[math]
[math]
(b) [math], [math].
Do the level curves of [math] and [math] cross at right angles?
[math]
[math]
| Use the contour diagram of [math] to decide if the specified directional derivative is positive, negative, or approximately zero.
1. At the point [math] in the direction of [math], 2. At the point [math] in the direction of [math], 3. At the point [math] in the direction of [math], 4. At the point [math] in the direction of [math], 5. At the point [math] in the direction of [math], 6. At the point [math] in the direction of [math], |
 (Click graph to enlarge) |
Note: You can earn 50% partial credit for 4 - 5 correct answers.
| Each diagram represents the level curves of a function. For each function, consider the point above [math] on the surface [math]. (a) If the vectors below are normal to the surface at the point [math], match each vector to a diagram. 1. [math] 2. [math] 3. [math] 4. [math] 1. [math] 2. [math] 3. [math] 4. [math] |
(Click on a graph to enlarge it)
|
Note: You can earn 50% partial credit for 4 - 5 correct answers, and 75% partial credit for 6 - 7 correct answers.
If the gradient of [math] is [math] and the point [math] lies on the level surface [math], find an equation for the tangent plane to the surface at the point [math].
[math]
Consider the function
[math]
(a) Find [math].
[math]
(b) Find a function [math] whose level zero set is equal to the graph of [math] and such that the coefficient of [math] in [math] is [math].
The level set [math] [math] is the same as the graph of [math].
(c) Find the gradient of [math]. Write your answer as a row vector of the general form [math].
[math]
(d) Use [math] to find a vector [math] perpendicular (or normal) to the graph of [math] at the point [math]. Write your answer as a row vector of the general form [math].
[math]
(e) Find an equation for the tangent plane to [math] at the point [math]. Enter your answer as an equation.
Note: You can earn partial credit on this problem
留言列表
STM32 (1)
